1. 贝叶斯定理(Bayes’ Theorem)
英国数学家托马斯·贝叶斯(Thomas Bayes)在1763年发表的一篇论文中,首先提出了这个定理。
1.1 条件概率公式(Formula of Conditional Probability)
P(B): 指发生事件B的概率;P(A|B): 指在事件B发生的情况下,事件A发生的概率;P(AB): 同时发生事件A和B的概率, 有的记为P(A∩B);
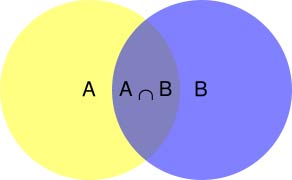
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(AB)除以P(B)。
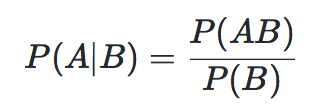
因此: P(AB) = P(B)P(A|B) ,同理: P(AB) = P(A)P(B|A)
这就是乘法公式 :
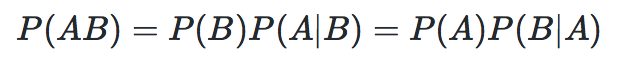
乘法公式的推广: 对于任何正整数
n≥2,当P(A1A2...An-1) > 0时,有:P(A1A2...An-1An)=P(A1)P(A2|A1)P(A3|A1A2)...P(An|A1A2...An-1)
根据乘法公式: P(B)P(A|B) = P(A)P(B|A)
即可以得到条件概率公式:
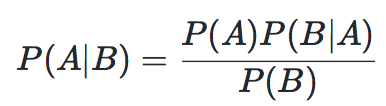
设互斥事件 A1,A2,...An 是样本空间Ω (Omega)的一个划分,B为任一事件,则广义的条件概率公式为:
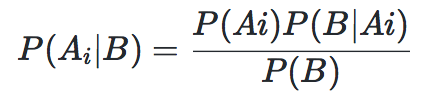
1.2 全概率公式(Formula of Total Probability)
假定样本空间S,是两个互不交叉事件A与A’的和。
当事件B发的概率即为 B和A及A'相交 的部分,即: P(B) = P(BA) + P(BA')
由上节推导可得: P(BA) = P(B|A)P(A)
从而得到全概率公式:
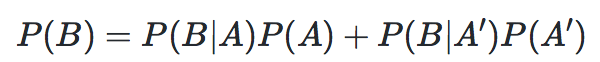
全概率公式的含义是,如果A和A’构成样本空间的一个划分,那么事件B的概率,就等于A和A’的概率分别乘以B对这两个事件的条件概率之和。
设互斥事件 A1,A2,..An 是样本空间Ω的一个划分,B为任一事件,则广义全概率公式为:
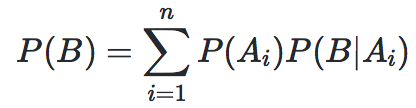
全概率公式的意义在于,当直接计算P(B)较为困难,而P(Ai),P(B|Ai) (i=1,2,…n)的计算较为简单时,可以利用全概率公式计算P(B)。思想就是,将事件B分解成几个小事件,通过求小事件的概率,然后相加从而求得事件B的概率。
将事件B进行分割的时候,不是直接对B进行分割,而是先找到样本空间Ω的一个个划分 A1,A2,...An ,这样事件B就被事件 BA1,BA2,...BAn 分解成了n部分,即 B=BA1+BA2+...+BAn, 每一Ai发生都可能导致B发生相应的概率是P(B|Ai)。
实例:某车间用甲、乙、丙三台机床进行生产,各台机床次品率分别为5%,4%,2%,它们各自的产品分别占总量的25%,35%,40%,将它们的产品混在一起,求任取一个产品是次品的概率。 解:
P(B) = 25%*5% + 4%*35% + 2%*40% = 0.0345
1.3 贝叶斯公式(Bayes Formula)
与全概率公式解决的问题相反,贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因.
根据条件概率公式和全概率公式可以导出贝叶斯公式:
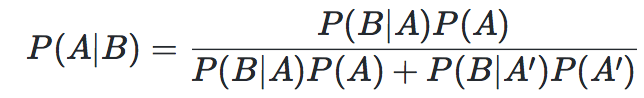
设互斥事件 A1,A2,...An 是样本空间Ω的一个划分,B为任一事件,则广义贝叶斯公式为:
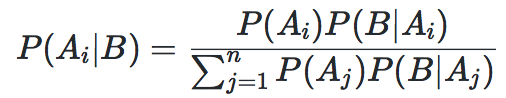
实例:发报台分别以概率0.6和0.4发出信号“∪”和“—”。由于通信系统受到干扰,当发出信号“∪”时,收报台分别以概率0.8和0.2受到信号“∪”和“—”;又当发出信号“—”时,收报台分别以概率0.9和0.1收到信号“—”和“∪”。求当收报台收到信号“∪”时,发报台确系发出“∪”的概率。解:P(A1|B)= (0.6 * 0.8)/(0.6 * 0.8 + 0.4 * 0.1) = 0.923
2. 贝叶斯推断(Bayesian Inference)
贝叶斯推断(Bayesian inference)是一种统计学方法,用来估计统计量的某种性质。贝叶斯推断与其他统计学推断方法截然不同。它建立在主观判断的基础上,也就是说,你可以不需要客观证据,先估计一个值,然后根据实际结果不断修正。
对条件 概率公式 进行变形,可以得到如下形式:
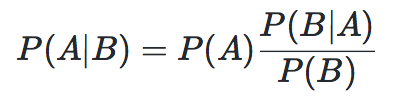
A被视为导致事件B发生的”原因”;P(A)称为先验概率(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断;P(A|B)称为后验概率(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估;P(B|A)/P(B)称为可能性函数(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
在这里,如果”可能性函数”P(B|A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”,意味着”先验概率”被削弱,事件A的可能性变小。
因为贝叶斯推断的主观性太强,曾经遭到许多统计学家的诟病。它需要大量的计算,因此历史上很长一段时间,无法得到广泛应用。只有计算机诞生以后,它才获得真正的重视。人们发现,许多统计量是无法事先进行客观判断的,而互联网时代出现的大型数据集,再加上高速运算能力,为验证这些统计量提供了方便,也为应用贝叶斯推断创造了条件,它的威力正在日益显现。
3. 实例
3.1 黑球白球问题
问题描述:A壶和B壶外表一样,A壶里有9个白球1个黑球,B壶里有2个白球8个黑球,现从其中一个壶取出一个球是黑球,那这个壶是A壶或B壶的概率分别多少?
首先, 根据理由不充分原理,设定相同的先验概率: P(A) = P(B) = 0.5
如果用X来表示摸出的球是黑色的,现在实际上要求后验概率 P(A|X) 和 P(B|X)的概率。 根据贝叶斯公式:
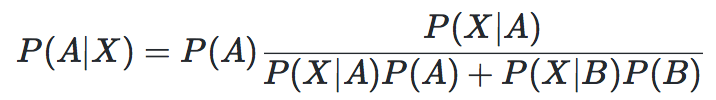
根据已知壶里的球的数量可知, P(X|A) = 0.1 , P(X|B) = 0.8 .
则当前这个壶是A壶的后验概率 P(A|X) = (0.5 * 0.1) / (0.1 * 0.5 + 0.8 * 0.5) ≈ 0.11
同理可求得当前这个壶是B壶的后验概率 P(B|X) ≈ 0.89
3.2 升级的黑球白球问题
问题描述: 接着上一个问题,将摸出的黑球重新放回这个壶中,重新取出一个球任然是黑球。这时候这个壶是A壶或B壶的概率分别多少?
贝叶斯推理符合 “序贯理性” 特性,即通过同时利用两个事件X1,X2求出的后验概率, 和将事件X1得出的后验概率作为事件X2的先验概率再求出后验概率,两者是完全一致的。
也就是说我们可以将上面计算的后验概率作为现在的先验概率: P(A) = 0.11, P(B) = 0.89
设再次摸出黑球事件用X2表示,则 P(X2|A) = 0.1 , P(X2|B) = 0.8 .
则当前这个壶是A壶的后验概率 P(A|X2) = (0.11 * 0.1) / (0.1 * 0.11 + 0.8 * 0.89) ≈ 0.02
同理可求得当前这个壶是B壶的后验概率 P(B|X2) ≈ 0.98
可见再次摸出黑球让黑球更多的壶的概率提升了。获得更多信息可以让贝叶斯推理更精确一些!
3.3 蒙蒂霍尔问题
问题描述:A,B,C三道帘子,其中一道帘子后面停着一辆轿车作为奖品。你选择其中一道,如果揭开后面有轿车,那么轿车就归你所有了。当你选了A后,主持人会从剩下两道帘子中,选择B帘打开,而B帘后面没有轿车。这时,主持人问你:现在只能从A和C中选择,你是否要改变主意?这时,你该不该改变最初的选择呢?
这个问题源于美国一个现场观众参加游戏的电视节目,节目主持人叫蒙蒂霍尔。这就是“蒙蒂霍尔问题”、“蒙蒂霍尔悖论”得名的由来。
首先, 根据理由不充分原理,设定相同的先验概率: P(A) = P(B) = P© = 1⁄3
设主持人打开B帘的事件为X,架设轿车在A帘后,主持人可以打开B帘或者C帘,则: P(X|A) = 1⁄2
如果轿车在B帘后,主持人是绝对不会打开B帘的,所以: P(X|B) = 0
如果轿车在C帘后,因为主持人不能打开观众选择的A帘,只能打开B帘,所以: P(X|C) = 1
根据贝叶斯公式,
P(A|X)
= ( P(A)P(X|A) ) / ( P(A)P(X|A) + P(B)P(X|B) + P(C)P(X|C) )
= ( 1/3 * 1/2 ) / (1/3 * 1/2 + 1/3 * 0 + 1/3 * 1)
= 1/3
同理可求得: P(C|X) = 2⁄3
根据上面分析,说明轿车在C帘后面的概率更大一些,你应该改变最初的选择。
然而事情并没有那么简单!如果轿车在C帘后面主持人会毫不犹豫选择打开B帘,如果轿车在A帘主持人可能在B和C之间稍微犹豫一下。聪明的游戏者会看穿主持人那一瞬间的犹豫,以此为线索推算轿车在那一个帘子后面。为避免这种情况,主持人可以事先准备好根据轿车位置来打开那一个帘子,并预先练习。比如轿车在A帘就开B帘,轿车在B帘就开C帘,轿车在C帘就开B帘。
则有: P(X|A) = 1 , P(X|B) = 0 , P(X|C) = 1
重新计算结果: P(A|X) = 1⁄2 , P(C|X) = 1⁄2 , 也就是说轿车在A帘和C帘的概率是一样的。
但如果将条件改为:轿车在A帘就开C帘,轿车在B帘就开C帘,轿车在C帘就开B帘。 , 则有: P(X|A) = 0 , P(X|B) = 0 , P(X|C) = 1 , 相应计算结果为P(A|X) = 0 , P(C|X) = 1 ,汽车百分百在C帘后。
可见,概率性推论存在“主观”因素,即对概率现象结构的想象,不同模型的构建方式会有不同的结论。